大規模ネットワークから有益な知識を抽出するための可視化技術の開発を目的としています。近年様々な分野でネットワーク構造が注目され分析の対象となっています。本研究は、分析的な応用を指向したレイアウト技術を開発することで、視覚的なネットワークの分析を支援することを目指しています。技術的な課題は、構造的特徴の把握に適したレイアウトのスタイルおよび可読性の基準を探り、定式化するとともに、その基準を満すレイアウトを効率的に求めるアルゴリズムを構築することです。
三末によるネットワークの可視化技術の解説記事がここにあります。



この研究は、スモールワールドネットワークを対象にそのグラフ構造の理解を助けることを目的としています。特に、大規模なクラスタに埋もれがちな中規模〜小規模な構造を顕在化させることに焦点を合わせ、ネットワークに構造的な分解操作を加えることで、それによって生じるレイアウトの変化を視覚的に提示する手法を提案しました。小規模なネットワークを利用した実験を通して、提案手法の特徴と有効性を示しました。(右の図はDBLPから抽出した共著関係のネットワークを可視化したものです。1は共著関係ネットワークをそのままスプリングモデルを利用して描いたものです。四つのクラスタがあることが分ります。そこで右側の最大のクラスタに着目し、そこの部分構造をさらに把握したいとします。2はSpanning Treeを取り出したものです。最大のクラスタはまだ密度が高く部分構造の把握は困難です。3は最大のクラスタの核となっているノードを削除した後にSpanning Treeを取り出したものです。このような操作を行うことで、最大のクラスタに隠れていた中規模〜小規模のクラスタが見えるようになりました。)
2部グラフによって表現される関係の視覚化を目的とし、その描画法の一つとして「アンカーマップ (anchored map)」の描画手法を提案しました。アンカーマップとは2部グラフの2種類のノードの一方に位置の制約を課した描画スタイルです。そのアンカーマップの描画法の基礎技術として二つの技術を開発しました。一つはアンカーノードの配置順序を決定するための指標、もうひとつはその指標を利用してアンカーノードの配置順序を決定するアルゴリズムです。いくつかの2部グラフのレイアウトをたくさん求め、美的基準に影響を与える属性値と提案した指標の関係を調査することで、開発した手法の有効性を評価しました。(右の図は酵母のタンパク質の相互関係を2部グラフと見たててアンカーマップとして描いたものです。左がランダムなレイアウト、右が提案した手法で求めたレイアウトです。右の方がすっきりとしていることが分ります。)


購買履歴データベースを対象にしてアンカーマップの描画を試みました。ここでの購買履歴データベースとは、一品の買い物が一つのレコードで表わされ、一つのレコードには、購入日、購入時刻、購入者(顧客名)、商品名、商品カテゴリ、価格が記録されているものです。現実の店舗のデータベースは入手できなかったため、研究室内での商品の購買履歴データベースを利用しました。研究室内に限定されてはいますが、現実の売買を記録したものです。2006年6月に稼働開始し、2006年末までの半年間に、2652件の購買が記録されています。その間の購入者数は18人で販売された商品は278種類になります。このデータベースから様々な関係情報を抽出することができます。たとえば、商品に着目すると、商品とそれを購入した人の関係、商品とそれが売れた日の関係、商品とそれが売れた時刻との関係などです。それ以外にも、購入者に着目すると、購入者と購入日の関係、購入者と購入時刻との関係なども抽出できます。
左の図では、時間帯を24個のアンカーとして配置し、対応する時間帯に購入された商品をフリーノードとして配置しています。時間帯は周期的な順序があるため、時計回りに配置しました。この図からすぐに分かることは、早朝から午前の時間帯の活動が低いということです(学生は午前中あまり研究室に来ません!)。さらによく見ると、カレーやスパゲティといった食品が夕食時間帯に特化して現れるのに対して、缶コーヒーやお菓子が特定の時間帯に依存せずに買われている「らしい」ことも分かります。
右の図では、左の図とは逆に商品をアンカーとして配置しました。商品には順序が無いため、アンカーの配置に工夫をしています。これにより、以下のような時間帯のクラスタが見えます。(1) 早朝1:04h、05h、06h、(2) 早朝2:07h、08h (ノードなし=活動なし)、(3) 午前:09h、10h、11h、(4) 昼食時:12h、13h、14h、(5) 夕方〜夜:15h〜03h。購買行動という観点での行動パターンのクラスタとして解釈することもできます。もちろん既存のクラスタリング手法を用いることで、このようなクラスタを(おそらくより高精度に)得ることはできますが、アンカーマップを用いることのメリットは、クラスタの背景(クラスタが構成されるに至った根拠)も同時に見ることができることにあると考えています。
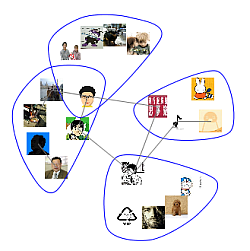
「複合グラフ」とは、2種類のエッジを備えるグラフを表現する手法で、2種類のエッジを「リンクによって接続された隣接関係」と「ノードを表す領域の包含関係」の異なる表現によって同時に表現する方法です。ここでは、ノードを表す領域を自由曲線(スプライン曲線)で表現するとともに領域の交差(インターセクション)を許容するレイアウト手法を考案しました。これまでの複合グラフのレイアウト手法の多くは、ノードを円や長方形などの規格化された図形によって表現しており固い印象を与えていました。ユーザインタフェースに用いるには自由曲線のような柔らかい印象を与えるものの方が適している場合があります。また、自由曲線を利用することで、空間効率の改善も目指しました。SNSにおける人間関係(友人関係とコミュニティへの所属関係)などの表現に利用できるものと考えています。
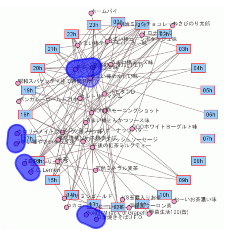
フリーノードのクラスタを見たいのであれば、いっそのこと領域線で囲んでしまおうということで、アンカーとの接続関係に基づく類似度(Jaccard係数)によってクラスタリングを行い、同じクラスタに含まれるフリーノードを閉曲線で囲んで表示することにしました。クラスタは階層的に構築されていますので、領域線も入れ子になります。
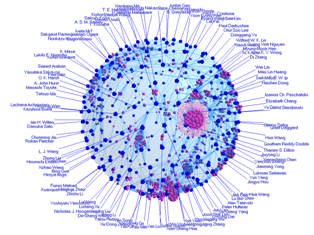
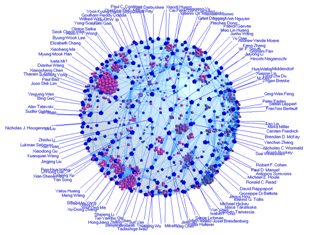
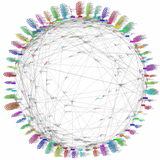
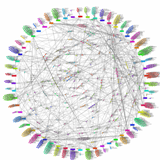
これまでに開発してきたアンカーマップは2次元の円周上にアンカーを配置していました。一般にバネモデルを利用するグラフ描画は2次元に(無理に)配置しているわけで、いろいろな所に歪みが生じます。そこで、2次元という制約を取り払い3次元への拡張を行いました。3次元に拡張するにあたり、円周の代わりに球面上にアンカーを配置しています(ちなみに、球面以外も試みています)。アンカーを円周上に配置する場合には、順序だけ決めれば良かったのですが、球の場合にはそう単純にはいきません。球面上にアンカーをできるだけ一様配置するために、そこでもバネモデルを利用しました。例は論文と著者の関係を描いたものです。青いノードのそれぞれが著者を表し、アンカーとして球面上に固定されています。紫系のノードが論文を表し、フリーノードとして共著者の重心付近に配置されています。実際にはマウスで回転させていろいろな方向から眺めることが可能です。
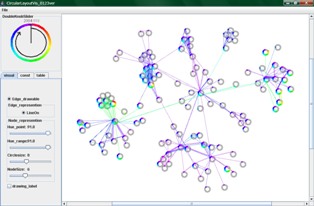
「動的ネットワーク」とは時間とともに変化するネットワークのことです。現実のネットワークは静的なものは稀で、むしろほとんどのネットワークが時間とともに変化します。このような動的ネットワークを視覚に表現する際の問題は、ノード間の位置関係をうまく表現するためには二次元(以上)必要である上に、更に時間軸を表現する必要があるということです。従来の代表的な方法には、アニメーション、配列表現、2.5次元表現などがあります。ここでは、時間変化も含めた一覧性を提供するために、2次元平面上に局所的な座標を設定し、それにより時間軸を表現する「環状配置手法」を開発しました。ノードの時間変化が環状のノードで表現されるとともに、色彩によって生存期間の表現を補足することで、ネットワーク全体の変化が捉え易くなっていると考えられます。